Chapter 1 - Basic Concepts of Pneumatics

What is pneumatics?

Pneumatics is the utilization of compressed air in science and industry in order to perform mechanical work and control. We can either talk about pneumatics or pneumatic systems.

In this course we define pneumatics as the control and transfer of power by using compressed air.

Advantages and Disadvantages of Compressed Air

Pneumatic systems have numerous advantages, the most important of which are:

• The medium, compressed air, can be easily extracted from our environment. There is no lack or shortage of it.

• After usage the compressed air goes back to its original condition. It can be released into the environment.

• Air can be compressed flexibly. Therefore it is ideal for absorbing shocks and vibrations.

• The distribution of compressed air can be easily handled with pipes and hoses.

• Compressed air can be used in fire- and explosion-hazardous environment.

• Both its pressure level and volume can be regulated quite easily. Therefore the energy brought to the actuator can also be controlled quite easily and within broad parameters.

• The usage of pneumatic components is easy as well as their maintenance. Their functionality is generally very reliable.

Besides these advantages there are some typical disadvantages:

• Compressed air – depending on its application – needs some preparation, especially filtration and drying.

• Because of pricy electric energy and the limited efficiency of compressors, compressed air is a relatively expensive means of energy.

• Because of air's compressibility, the precise and load-independent positioning of the actuator(s) is not possible.

Physical Fundamentals and Units of Measurement (metric system)

The SI-system of units is based on numerous basic and derived units of measurement. We do not cover that in detail. [International System of Units, short SI (french): Système international d’unités]

Units of measurement that are relevant in pneumatics:

• Meter – m (length / distance)
• Kilogram – kg (weight / mass)
• Second – s (time)
• Kelvin – K (temperature)

Derived units that are used:

• Newton – N (force)
• Pascal – Pa (pressure)

Force

Force is any interaction that, when unopposed, will change the motion of an object. In other words, a force can cause an object with mass to change its velocity (acceleration, change of shape). Force can also be described as a push or pull. It is a vector quantity consisting of magnitude and direction.

• Symbol: F
• Unit: Newton
• Unit symbol: N
• In SI-based units: 

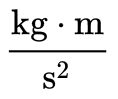
Pressure

Pressure is the force applied perpendicular to the surface of an object per unit area over which the force is distributed.

• Symbol: P
• Unit: Pascal
• Unit symbol: Pa
• In SI-based units:

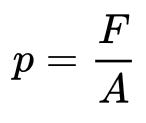
For measuring pressure, the following multipliers are common:

1 kPa (Kilopascal) = 1,000 Pa

1 MPa (megapascal) = 1,000,000 Pa

In pneumatics we normally use the unit bar.

1 bar = 100,000 Pa = 0.1 MPa = 0.1 N/mm²

1 mbar = 0.001 bar

1 nbar = 0.000000001 bar

In some countries such as the USA or Great Britain the unit psi (pounds per square inch) is also still in use.

1 psi = 0.07 bar (rounded)

Standard atmospheric pressure is the pressure of the air on sea-level, which equals 1 atm (atmosphere).

1 atm = 101,325 Pa = 1013.25 mbar (Millibar) or hPa (Hektopascal)

This unit is normally used in meteorology. Rounded and precise enough for most applications:

1 atm = 1 bar

Excess pressure or gauge pressure is the value of pressure above standard atmospheric pressure. It is also called relative pressure.

In case absolute pressure is measured, standard atmospheric pressure is included. The scale starts at 0 Pa = total vacuum.

Absolute pressure = standard atmospheric pressure + gauge pressure (relative pressure)

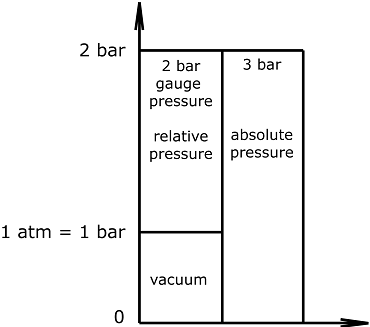
Expressions:

• P_(a): Absolute pressure
  
• P_(t): Excess/Gauge pressure
  
• -P_(t): Vacuum

 Examples:

• 6 bar excess pressure = 6 bar_(t)
• 7 bar absolute pressure = 7 bar_(a)
• 0.7 bar absolute pressure = 0.7 bar_(a) or -0.3 bar_(t)

The expressions „excess pressure“ and „vacuum“ refer to a value larger or smaller than standard atmospheric pressure.

There are different levels of vacuum:

In pneumatics we use the unit bar for vacuum as well as for excess pressure.

Unless there is any further indication, we normally work with excess pressure = relative pressure.

In practice:

We will calculate the force of a cylinder with a defined diameter at a specific pressure.

According to Pascal's law:

• p: Pressure [Pascal]
  
• F: Force [N]
  
• A: Surface [m²]

How much force does a cylinder with a diameter of 40 mm apply at a pressure of 6 bar?

In order for us to use the correct units of measurement, we will use the unit Mpa for pressure. This conforms to N/mm². For the diameter we will use mm.

Diameter of the piston of the cylinder
        

d = 40 mm

The surface of the piston is to be calculated as a circular area:

In numbers:

At a (relative) working pressure p = 6 bar = 0.6 (N / mm²)

Thus:

In numbers:

This is the theoretical force. In practice we have to take losses due to friction into consideration (approx. 5%).

Thus: A cylinder with a piston with the diameter of 40 mm at 6 bar pressure generates approx. 716 N force. This translates into the ability to lift approx. 73 kg.

How much force does the same cylinder generate into the opposite direction (pulling its rod back in)?

Due to the piston rod itself, the surface to push the rod out is larger than the surface to pull it back in. The missing surface hast to be deducted.

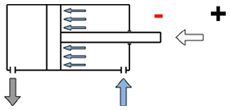
D = diameter of piston               (40 mm)

d = diameter of piston rod          (16 mm)

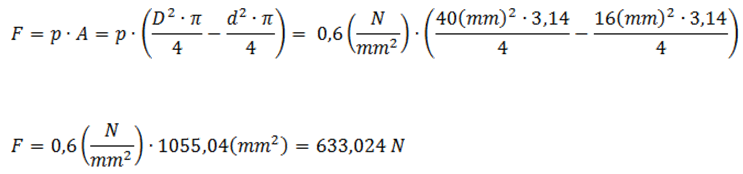
After deducting 5% as loss for friction we find that the pulling force of the same cylinder is approx.

601 N, in comparison to the 716 N pushing force.